在六西格玛项目开展过程中，我们一直强调数据的分析，而回归分析正是对数据分析的重要工具。

     当一个因变量Y可能由多个因子X’s共同作用时，多元回归的使用，很好的解决了这个问题。多元线性回归方程在建立回归方程后，进行统计分析，考察模型的显著性，进行残差分析，找出显著性的因子。

    一元回归或者多元回归分析中，其因变量Y一定是是连续型随机变量。在实际问题中，响应变量Y可能是离散型的，我们对离散型的Y一般可以用比率检验或者卡方分析，但对多个原因共同作用时缺少分析工具。此时我们会用到离散变量的Logistic回归（下文写为逻辑回归），逻辑回归中因子可能有连续型的，也有离散型，

逻辑回归中Y只有合格或者不合格，例如生产过程中的不良率等，下面重点介绍如何使用MiniTab来进行逻辑回归分析。

1、某项目组在研究焊接过程中的问题，该问题的Y为焊接气孔不良，项目组在初期分析过程中，认为焊料的品牌(离散型：A牌和B牌)、焊缝的大小（连续型）、焊接速度（连续型）可能对气孔不良有影响。

2、由于历史数据暂缺，项目组决定使用DOE的方式收集数据。

3、相关信息如下：

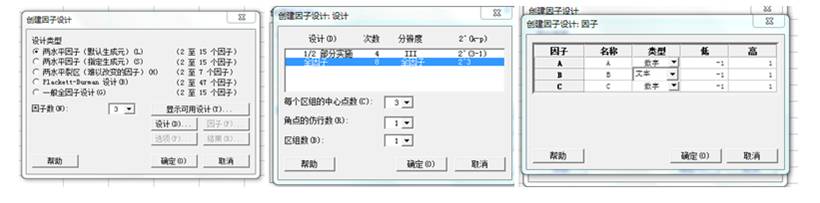
4、由于实验成本不高，项目组使用3因子2水平加3个中心点的全因子设计（每次试验为焊接200个），相关数据步骤及生产的DOE表单如下：   

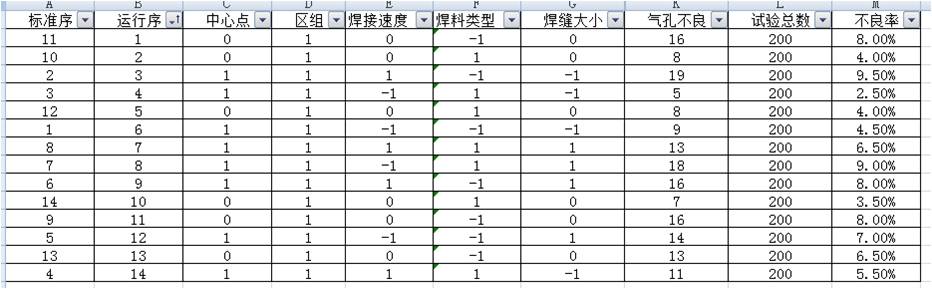
5、对相关试验数据进行收集，结果如下：（由于不良率为离散数据，不可直接用DOE分析）

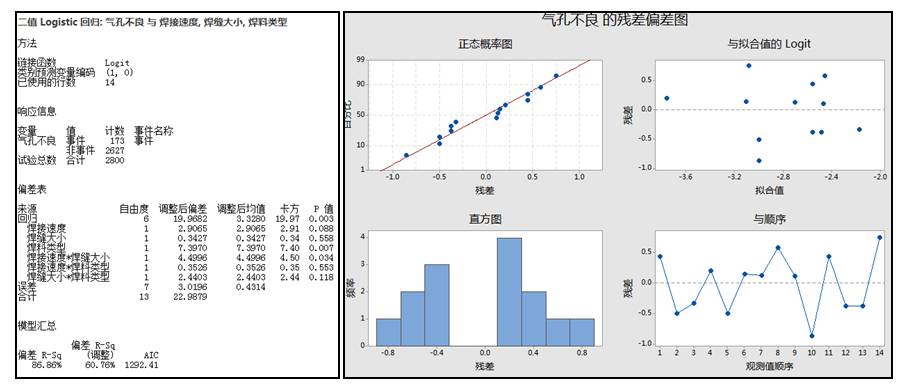
6、然后我们进行Logistic回归分析(相关设置如下)

以下为逻辑回归分析结果，模型总体是有效的，焊料类型、焊接速度*焊缝大小为显著项，残差图无明显异常。

同时我们可以利用逻辑回归分析中等值图观察到最佳区域，并使用响应优化器找到最佳水平为焊接速度80,焊料类型A牌，焊缝大小为0.02，此时预测最佳结果为2.28%.

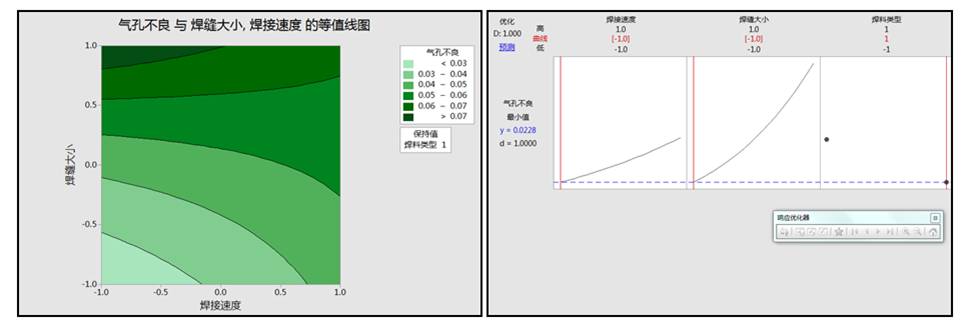
通过以上分析最佳的水平为选择焊料A品牌，焊接速度与焊缝选择低水平为该项目的最佳搭配，分析完成后应当重复试验确认分析结果的正确性。