在单值移动极差图（I-MR Chart）中，包含了两个图：一个图示单值图(I Chart)，一个移动极差图（MR Chart）。单值图：单个数据值的标点。移动极差：在单值图上连续两点的差异标注在图上，就是移动极差。

控制图实例如下

单值移动极差图（I-MR Chart）的假设是：

• 数据为计量型数据；

• 每个数据点都是独立的；

• 数据没有子组；

• 数据来源于正态分布；

• 如果非正态，那么也需要接近对称。

   

如果假设不成立，那么会导致错误的解释和结果。所以我们在选用单值移动极差图前，首先要确定我们获取的数据是彼此不相互影响的、不存在子组的且要经过分析数据正态分布的（数据的正态性检验见—）。接下来，我们以一个实例介绍如何利用Minitab制作单值移动极差图。

实例：

一家保险公司，目标是在30天以内完成承诺的保险业务。其中其关键的X是出发票到完成业务所耗用的时间。为了了解近8个月从处发票到完成业务耗用的时间是否存在异常。我们调取了近8个月的相关数据，期望通过控制图来分析该时间是否受控。相关的数据如下：

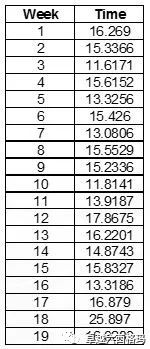
由于数据是计量型的且没有子组，故我们使用的是单值移动极差图。在使用Minitab之前，我们有必要利用该例子解释一下单值移动极差的特征。如下图：

第一组的移动极差因为需要后一个数据减去前一个数据，故在本例中不存在。第二个移动极差为0.93=15.3366-16.269，该数据将会标注在移动极差图的第一个点上。数据耗用的时间将会作为单值图的Y轴。横轴为不同的周数。移动极差图中的Y轴就是我们计算出的移动极差。耗用时间的平均值作为单值图的绿色的线。移动极差的平均值作为移动极差图的绿色线。

单值图和移动极差图的控制限是根据一系列统计公式计算出的，但在目前，我们可以不用过多关注如何计算，充分利用好统计软件的作用，从而有效提升解决问题的效率，故在此我们不会对相关的计算公式进行介绍，仅介绍如何使用Minitab分析本例。相关数据如下：

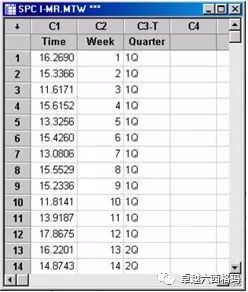
利用Minitab做如下选择步骤：

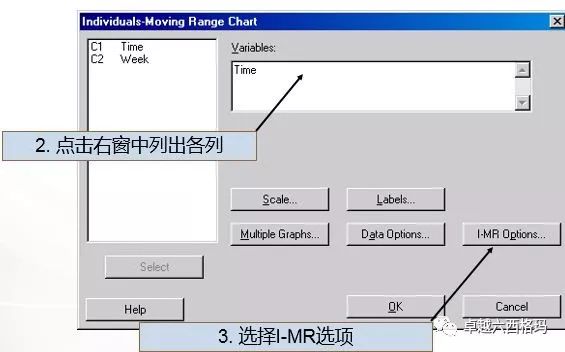
结果显示如下： 

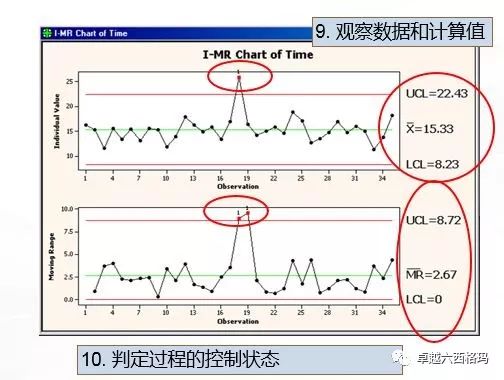
解释和分析：

肉眼观察：确保图形看着正常，图形对称，控制限大概接近于±3s

看Minitab的检验结果：图形中有超出控制限的点（单值图和移动极差均有）。在对话框中也同样说明了图形中存在失控的点，且明确了具体失控的是第几个点。本例中，单值18个点出现异常（超出上控制限）。移动极差在18和19的点上出现了异常（超出控制限）。

在单值移动极差图中，我们还可以利用其另外一个功能（利用数据分层的概念，参见   4、数据的分层）用于区分不同阶段的控制图的趋势的变化。这一功能在改进阶段后期比较常用，主要是用来比较改进前后的效果差异。

还是以本例数据为例，将不同的周数（横轴）以每季度作为数据分层的标准做单值移动极差控制图。具体步骤如下：

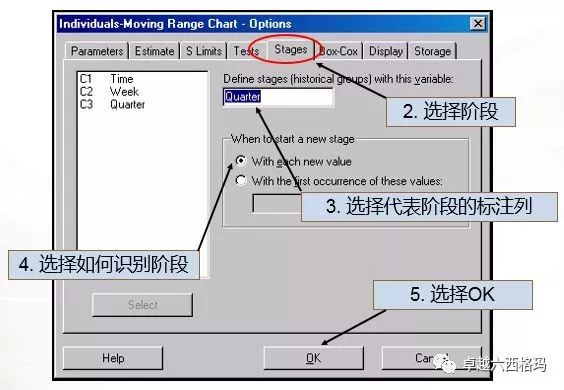
从阶段的图中，我们可以看出，不同分层的阶段（季度）表现出的过程是不一样的。在本例中的第二个季度的数据并不稳定，在19周的数据明显异于其他季度，导致第二季度的数据出现异常。此时，我们可以分析在第二个季度的第19周的数据出现了什么样的异常情况，并由此找出原因进行改进。

在单值移动极差控制图的使用过程中会遇到各种各样的问题，以下是比较容易出现的问题：

"瞥一眼"的方法会避免I-MR的滥用。比如：

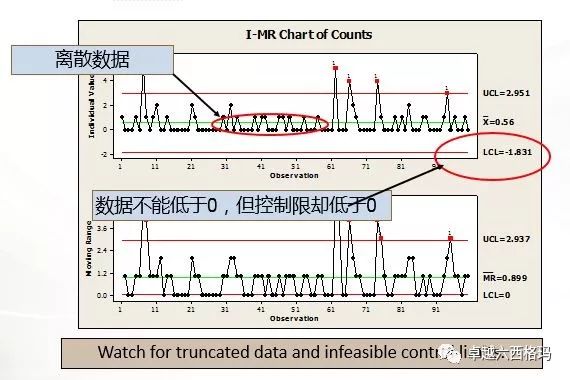
1.  出现了“离散“或”跳跃“的情况。且出现了控制限不能为零但实际却出现负数的控制限。

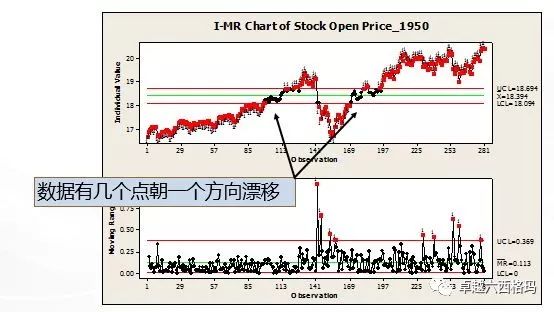
2.  非独立数据。数据会朝着某一个方向漂移；

3.   出现了非正态的数据，主要的表现就是低值或高值的分布过密。这时，我们要利用正态性进行数据的检验，看是否数据呈正态分布（参见  第11期 数据的正态性）

如之前的介绍，单值移动极差图可以用于评价过程是否处于受控状态，即：通过数据组的控制图看是否有失控的存在，如果存在失控，则需要我们尽快查找原因，直至针对原因的行动实施后再次评价数据的稳态。如果此时过程没有失控，则可以利用该控制图的上下限对过程进行单值和移动极差的控制了。如果在未来的某一个点出现了失控，我们就可以知道过程由于异常原因导致过程不稳定了，并由此提前预见未来可能出现的不合格的输出！

学习六西格玛请添加老师微信：newlifes008