说起测量系统分析MSA,个人认为是IATF五大工具中最难的。这个难主要体现在理论和实践两个方面,一是涉及到不少统计学知识点,如假设检验、回归分析、T分布、F分布、P值判定、ANOVA等;另一方面在实践中难以按照MSA手册要求执行有一堆问题难以把握重点,比如做MSA之前以下问题我们是否考虑过以下问题:
1、什么是测量系统?
2、为什么要做测量系统分析(MSA)?
3、MSA需要考虑到哪些内容?MSA就是做GRR吗?
4、GRR的结果是怎么得出的?
5、Minitab的GRR输出结果怎么看?
6、GRR结果大于30%的测量仪器就不能用吗?
本文将避开统计学知识(这些知识我也差不多都还给老师了),用比较简单的计算推导从一个实例详细介绍GRR方法是如何评估一个测量系统的精确度,以及回答以上几个问题。为了能让人看下去,本文涉及的相关计算只需要初中水平的数学知识,如果还是无法搞明白的话….呃….最近发现有家网红火锅店高老九很赞,要不出去搓一顿吧。
闲话少说,言归正传。先解释下什么是测量系统,这个大家都比较熟悉了:测量者、测量仪器、测量方法、被测量的样品、甚至测量环境共同构成了测量系统。为什么要做测量系统分析呢?测量系统分析和我们常说的测量不确定度两者之间关系如何?IATF的MSA手册说的很好,我就直接放上来虽然抄袭是可耻的:

生产制造过程是存在变异或者说是波动的,数学上用方差来表示。我们关心这个过程的变异因为我们希望生产制造过程是稳定受控的而且过程变异比较小。我们得到的过程变异(方差)是测量所得,显然包含过程本身的变异以及测量所带来的变异,那么其中由测量系统产生的变异所占比例多大?会对过程波动的结果判定产生影响吗?产生多大的影响?这是测量系统分析所要解决的问题。现在一提MSA,很多人就直接理解为GRR(Gage Repeatability &Reproducibility),实际上按照MSA手册定义,我们需要系统考虑测量系统的五性:稳定性,偏倚,线性,重复性,再现性。稳定性是进行测量系统分析的基础与前提,是最重要的特性也是以往最被忽略的;偏倚和线性反应测量系统的准确性,我以前文章介绍过偏倚以及假设检验,大家有兴趣可以看一下;重复性和再现性反应的是测量系统的精确性,也就是我们熟知的GRR。稳定性、偏倚、线性的结果要用到一些控制图和统计学知识,比如假设检验、回归分析来解释,所以大家觉得麻烦啊。然而GRR结果很直观,哪怕没有相关软件,直接网上下载专门的Excel表格(极差法)输入原始测试数据后,很轻易的就能得出结果,而且结果很容易解释,PV%或PV/T%大于30%就不可接受。GR易于结果判定的优点使得很多人一提起MSA就认为是GRR。本文紧跟潮流,主要介绍GRR方法是如何评估一个测量系统的精确度。GRR主要思路是将我们测量所得的产品过程的波动(以方差表示)分解为产品本身的波动、测量仪器的波动(重复性误差)、测量人员波动(再现性误差)等,然后计算测量本身的波动(重复性和再现性)在整个测量所得的产品过程的波动所占的比例。MSA手册给出分解图如下:
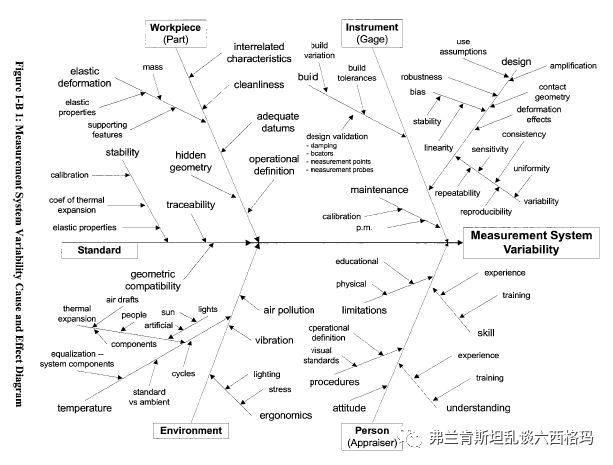
我们看一个具体的实例:在实际工作中,某产品为流程性的浆料,产品的特性是粘度需要每批次进行检测。安排GRR分析实验时选取五个批次的该产品(p=5),两个测量员(n=2),每名测量员对每批次产品重复测试三次(r=3),测试结果如下,单位为CP.S,产品公差范围为20CP.S。
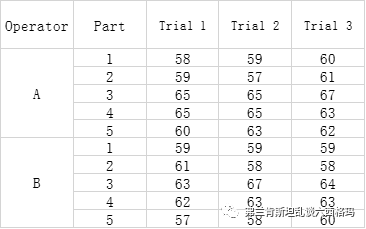
为尽可能消除测试重复性误差的影响,一般要求np≥15,pr≥15,本例中np=10低于要求但并不影响计算以及结果判定。进行GRR计算时MSA手册推荐极差法和方差分析法(ANOVA),极差法计算简单但是无法进行交互效应的判定,而且从本质上说极差法是用极差估计标准差,而标准差不满足线性计算要求,只有方差可以,这个之后本文会介绍。方差分析法的缺点在于计算麻烦需要借助相应分析软件。本例中我们利用Minitab软件轻松得到以下结果:
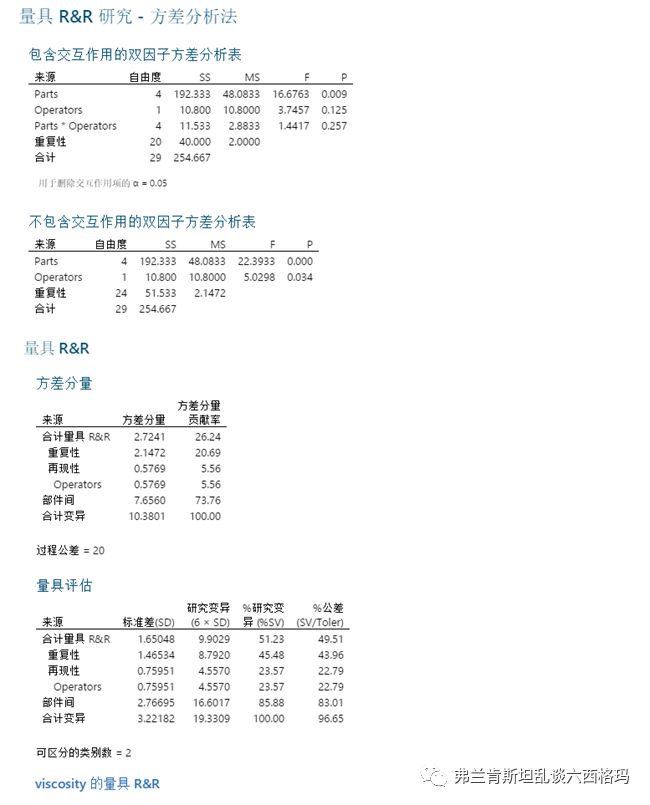
接下来花些篇幅解释下方差分析法的计算思路如何得出以上结果的。首先计算所有数据的离差平方和如下,测试员A的第一个测试样品的第一次测量结果的离差平方和为(58-61.333)的平方在结果表格中表示为红色字体11.111:
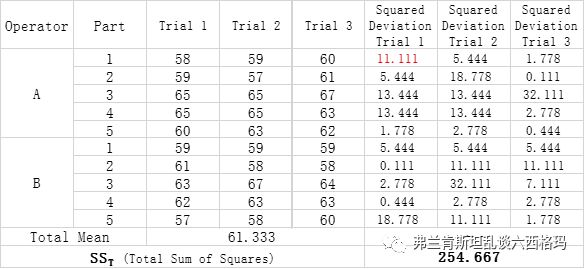
254.667是所有测试结果的总的离差平方和,总的自由度为30-1=29。第二步考虑部件之前的离差平方和,见下表,计算过程类似:
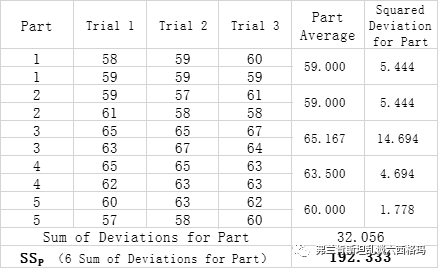
每个批次的样品重复测试6次,所以批次间的总离差平方和是32.056*6=192.333,对应批次间的自由度为5-1=4。第三步考虑测试人员间的离差平方和,每位测量员测试15次,人员间的离差平方和是0.72*15=10.8,人员间的自由度为2-1=1,见下表:
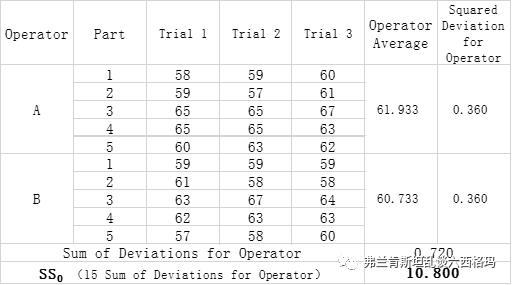
接下来第四步计算重复性测量的离差平方和,结果如下:
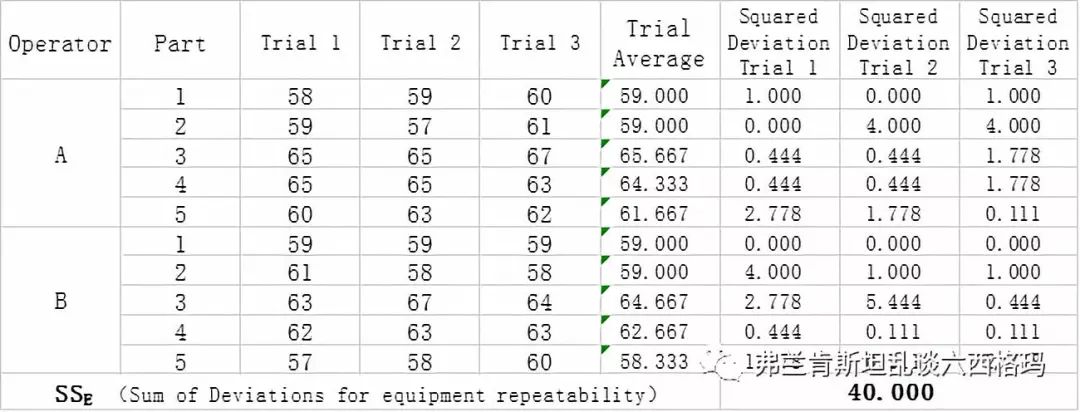
注意到与之前各分量的平方和计算不同,均值取得是每位测试员针对每个样品的三次重复测量的平均值,而不是所有测量结果的平均值61.333,自由度为10*(3-1)=20。由平方和分解公式:
 ,得出测量人员与部件间交互作用的离差平方和为254.667-192.333-10.8-40=11.534,对应自由度为29-4-1-20=4,至此所有总的与部分离差平方和以及对应的自由度计算完毕,见下表:
,得出测量人员与部件间交互作用的离差平方和为254.667-192.333-10.8-40=11.534,对应自由度为29-4-1-20=4,至此所有总的与部分离差平方和以及对应的自由度计算完毕,见下表:

看一下以上手动计算与Minitab软件计算结果,两者相同。如下图:
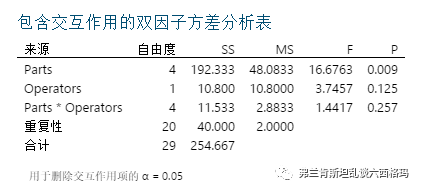
Minitab软件对测量人员与部件间交互作用进行显著性检验,这部分涉及假设检验,F分布,显著性水平的P值判定,需要一些数理统计学知识,这里一两句话说不清楚,有机会下次介绍。从结果上看P值0.257大于显著性水平0.05,所以判定不存在测量人员与部件间交互作用,把测量人员与部件间交互作用的离差平方和分量计入测量重复性误差,Minitab软件给出简化后的计算结果如下图:
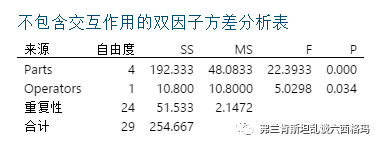
下面由以上各分量的平方和计算结果得出各部分的方差分量,首先是测量的重复性误差带来的方差分量:

接下来看由不同操作人员带来的再现性的方差分量:

注意到方差分析结果得到的操作人员变异的均方和包含对多个样品重复性测量的方差分量,所以需要扣除这部分。同理得出样品间的方差分量为:
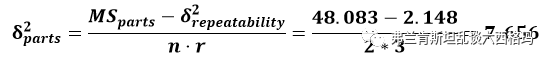
我们所观测到的过程总的变异,用总方差表示为:
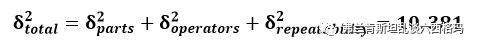
我们的计算结果和Minitab以下输出的结果是一致的:
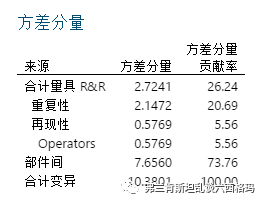
请注意方差分量所占百分比一栏,测量系统方差所占总方差的百分比为26.24%,为重复性方差分量所占总方差分量(20.69%)与再现性占比(5.56%)之和;总方差(100%)为测量系统方差分量占比(26.24%)与样品间本身波动的方差分量占比(73.76%)之和,与之前计算结果
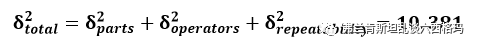
对应,用数学语言描述为:方差满足线性运算关系,总方差与各个分量的方差之间可直接进行加减运算。
由上一步计算出的各部分方差分量开根号得出各部分的标准差分量,再进行百分比计算,由此Minitab进一步给出MSA手册所要求的计算结果如下图:
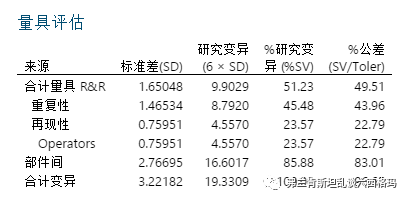
计算过程比较简单不多解释,一般而言我们就得出GRR的最终结果PV%和PV/T%分别为51.23%和49.51%,按照MSA的判定标准(PV%和PV/T%均小于30%为可接受),此测量系统显然是不可接受的,需要立即改进。从结果上来看,重复性带来的影响比较大,如何采取相应的措施,MSA手册中给出了详细的指导,这里不再赘述。
但是等一下,我们再看一眼计算结果,以上结果以标准差的百分比表示的话,重复性所占比例为45.48%,再现性为23.57%,两者之和并不等于测量系统所占比51.23%;而测量系统所占比51.23%与样品所占比85.88%,两者之和并不等于100%。原因在于标准差不满足线性运算关系,总标准差与各个分量的标准差之间不能直接进行加减运算。这个不难理解,好比勾股定理中,我们得出3的平方加上4的平方等于5的平方,但是3加4显然不等于5。MSA手册对此的描述只用一句话:

然后,就没有了,既没有说明为什么不等于100%,也没有说明对我们的结果评估有哪些影响,真是惜墨如金啊。我到现在也没搞明白,为什么AIAG会采用标准差计算各分量的百分比?可能是由于标准差和测量值有相同的量纲吧,但是以百分比又是无量纲的,而且百分比按正常直觉是满足线性运算关系的,也就是总和加一块肯定是100%,标准差的百分比计算显然违反这个正常逻辑。这个问题本文最后还会谈到,姑且先这样,我们再来解释一下文章一开始Minitab软件输出的图形结果。
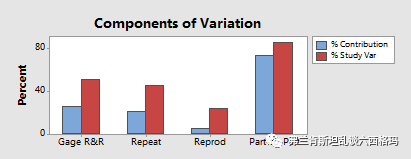
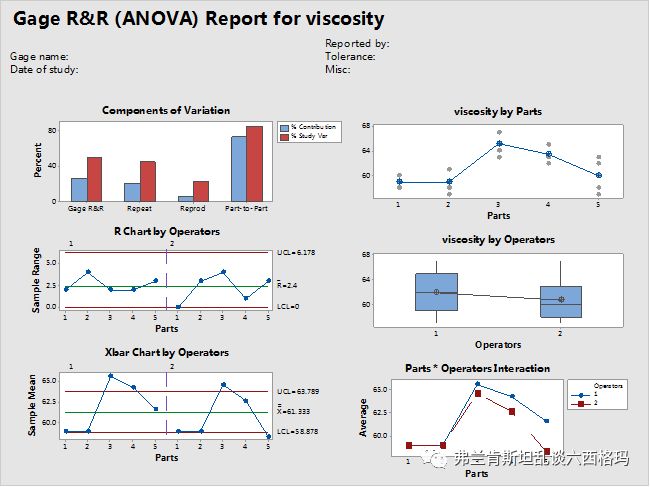
左上图代表各部分的方差分量(蓝色)与标准差分量(红色)的百分比,注意到GRR与Part to Part的蓝色柱体之和为100%,而红色柱体之和是大于100%的。
接下来是R图和样品均值图
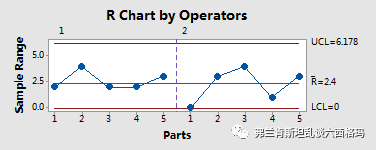
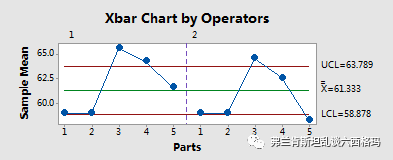
根据第一张图得出5个样品由2位测量人员重复测量3次结果的极差值的平均值为2.4,由此可计算出第二张图的上下控制线为:
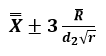
其中样品均值61.33,d2查系数表可得1.693,r为3,计算结果即为图中的UCL和LCL。注意和一般SPC控制图要求数据落在上、下控制限之内不同,此处控制限由对同一样品的重复测量误差决定,而不是由样品之间的差异(极差)决定,所以好的测量系统需要使测量结果尽可能落在上、下控制限之外。落在控制限之内则说明测量结果之间的差异可以用测量的重复性差异来解释,这是我们所不希望看到的。最后来看右下方测量人员和被测样品间交互作用图,
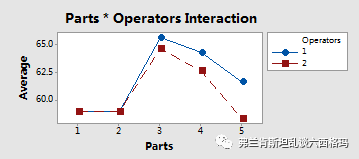
红线和蓝线接近于平行,所以不存在测量人员和被测样品间的交互作用。当然更严格的判定由P值检验结果决定,Minitab之前的输出的P值为0.257,大于判定阈值0.05,所以不接受交互作用存在的假设。
目前为止我们已经对本文开头的问题1-5做出了回答和解释,最后一个问题超出了MSA本身范围。我们再回顾一下本例的GRR结果,无论是测量系统变异占过程变异的PV%(51.23%)还是测量系统变异的6倍(为什么是6倍?)与规格限的比值PV/T%(49.51%)都大于MSA的要求(30%)。一般按照MSA的判定,这样的测量系统肯定是不合格,需要改进。但是不要被51.23%的数值吓到,因为这并不代表产品间的变异(过程真实的变异)是48.77%,实际上Minitab计算的结果告诉我们后者是85.88%。原因之前重点提过:标准差之间不满足线性计算关系,只有方差可以!测量系统变异的方差占总变异的26.24%,对应产品间的变异(过程真实的变异)是73.76%。一个变异占过程总变异26%的测量系统肯定不能使用吗?我们看之前输出的样品测量均值控制图,有测量值落在控制限之外,证明这个测量系统是有能力识别样品之间差异的!
Dr. Donald Wheeler在他的书中Evaluatingthe Measurement Process & Using Imperfect Data解释了这个问题,他的新方法也被应用于一些统计学软件如JMP中。下面简单介绍下他的思路。首先他定义了一个相关系数,
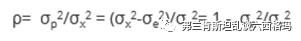
表示为产品间的变异(方差)与总变异(产品间的加上测量系统引入的)的比值,应为产品间的方差不容易得出,所以也可以写作1减去测量系统方差与总方差的比值。按照这个比值的大小,Dr.Donald Wheeler将测量系统分为4类,见下图:

其中涉及的判定准则如下:

我的英文很渣也就懒得翻译了,反正能看到这里的伙计应该都比较熟悉SPC了,这和SPC的8条判异准则基本差不多。按照我们之前的计算结果,测量系统变异的方差占总变异的26.24%,也就是相关系数ρ=1-0.26=0.74,可以归类为第二级的测量系统。当产品波动超过±3δ时,这个测量系统有超过88%的可能性仅凭借准则1就识别出了过程变异,是很可靠的测量系统!当然,处理第一级的测量系统,Dr.Donald Wheeler也建议第二级、第三极的测量系统采用控制图对测量系统本身的稳定性进行控制。最后我们再来看下上面表格最右侧一栏追踪过程改进的能力是什么意思。利用本例中的数据,产品公差范围为20CP.S,过程总的变异的标准差为3.222,过程能力
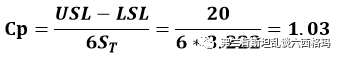
,按照Dr.Donald Wheeler提供的计算方法,我们利用本例Minitab输出的数据简单计算结果如下:
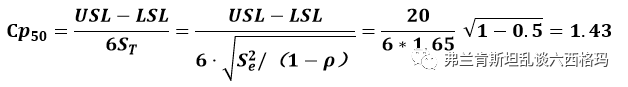
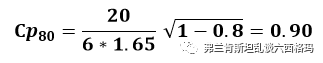
也就是说,当过程能力由当前的1.03提高到1.43时,当前的测量系统识别过程差异的能力下降,由第二等级降到第三等级;当过程能力由当前的1.03下降到到0.90时,当前的测量系统识别过程差异的能力提高,由第二等级升到第一等级。测量系统的能力评估不再孤立,需要与过程能力结合在一起进行动态评估。
总结:
1、测量者、测量仪器、测量方法、被测量的样品、甚至测量环境共同构成了测量系统。测量系统分析包括稳定性,偏倚,线性,重复性,再现性。GRR分析考虑的是测量系统的重复性,再现性。
2、GRR分析可采用极差法和ANOVA方法,后者思路是分解总的过程变异为样品间、测量者间、重复测量间的变异,MSA手册用标准差定义这些变异,用Minitab软件可以轻易计算出结果。
3、GRR方法的标准差运算不满足线性关系,对于PV%大于30%均判定为测量系统不可接受。实际本例PV%在51.23%的情况下仍可以识别出过程变异。采用Dr.Donald Wheeler新的测量系统的评估方法可以对此作出解释,并且可将测量系统能力的评估与过程能力本身结合起来。







