上一章节,我们同大家探讨了品质的基本概念、数据类型、以及描述数据分布形态的几个关键名词。今天同大家分享的是计量型数据中使用非常广泛的一个工具-工程能力-CPK,SIX SIGMA的改善工作就是持续推进工程能力向2.0无限接近的过程。
上一章节我们谈到通过μ,σ来表示母集团数据分布的状态,这样的操作是可取的,但在使用中的弊端也是很显而易见的,那就是从这两个数据的描述是不能较为直观的知道数据相对于管理规格的符合程度。而工程能力CPK这一个数据,它综合了μ,σ融合到计算公式内,通过同分布的sigma水平相对应,我们能很清晰的看出数据被不良比例。

对一个特定的工程,给定的公差范围作为分子(即产品允许的公差带),抽样的实际散布状态S作为分母,这个比值称之为潜在的工程能力,也就理论上特定散步条件下样本可能达到的最大工程能力。这个比值越大,说明样本的散布越小,个体的差异越小,可能的良品率越高。

但这样的分析是没有考虑样本均值X-BAR同母集团均值μ重合、偏移关系下进行的评估,因此存在明显的可靠性不足。

如上两个图,我们按照前面的工式进行计算,两者的CP是一致的。但是,很明显上图的数据均值同规格中心重合,下图数据中心向右偏移了一个σ水平,但下图理论计算的CP还是会同上面的图形一致。实际工程中,这样两种分布状态,真实的不良率是存在显著的。
因此,为了弥补CP评价样本面貌的不足,引入另个一个概念:短期工程能力。将规格上限、规格下限和散布水平纳入评价。分别得到了CPU:潜在上限工程能力,潜在下限工程能力 CPL(详细算法参考下图的公式),而将两者中数值小的那个称之为:短期工程能力CPK。通过这样的计算,巧妙的将均值、散布、规格中心,融合在一起,无论样本数据如何变化,都能通过这一公式,很直观准确的评估数据的面貌。
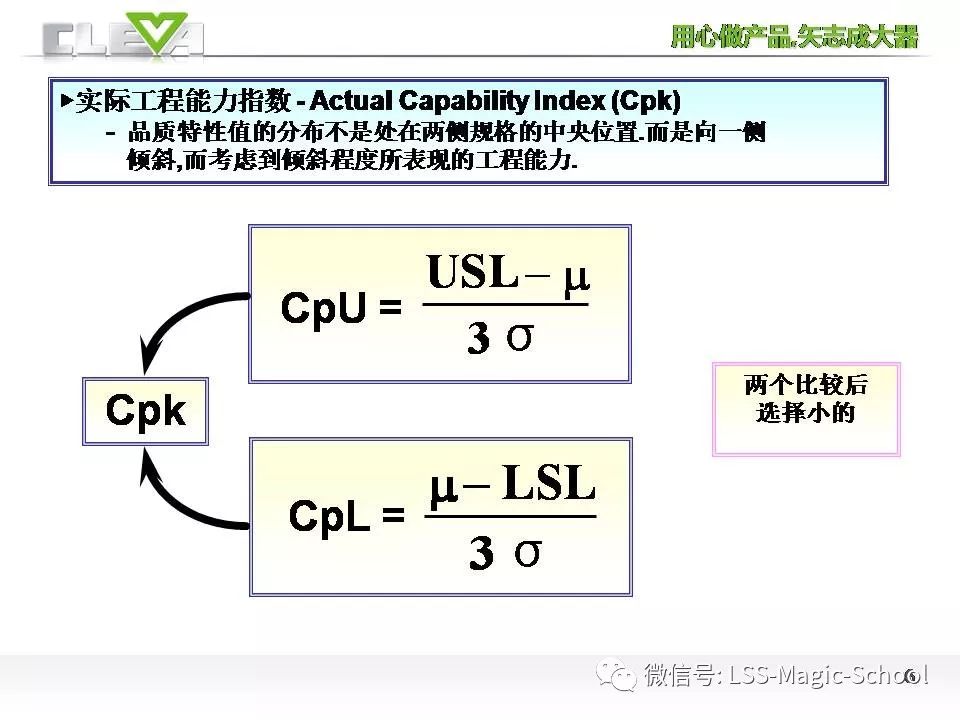

因为样本中心最佳的分布状态就是中心同规格中心重合,而实际上的数据往往不会和规格中心完美重合,因此基于CPK的公式,大家很容易发现CPK永远也不会比CP大。
没有深入学习SIX SIGMA的人,也会听到很多关于CPK=1.0怎样,1.33怎样,1.66有怎么样,2.0又怎么样的说法。为了便于理解,我们制作了如下图形,供大家自学。请大家通过观察图形,结合前面谈到的公式,进一步的理解工程能力的呈现的数据面貌。

最后,抛出2个开放式问题:1、CPK可以是一个小于零的负值吗?
2、CPK=2.0意味着什么?
欢迎大家提问互动,本期的提出的2个问题点,下期我们进行一一解答。
如果您想学习六西格玛可以添加讨教大学老师微信:newlifes008







