ISM基本思想是：通过提取问题的构成要素，利用有向图、矩阵等工具，对要素及其相互关系等信息进行处理，最后用文字加以解释说明，从而明确问题的层次和整体结构。其实施流程如下图所示。

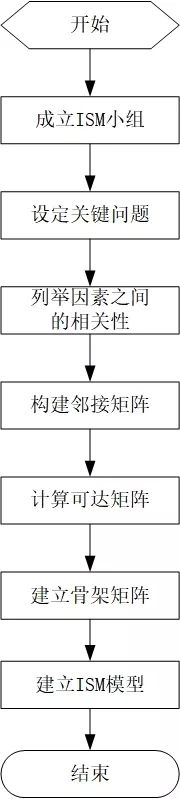
▲ISM实施流程

(1)成立ISM小组。解释结构模型主要以定性分析为主，针对使用者而言，如果其在能力以及积极性方面存在差异，那么最终所得到的效果也会存在差别。通常情况下，在对结构模型法进行实际应用时，需参与的人员主要有三种，其一为掌握有建模核心知识及方法的专家，其二为用于协调各环节的协调人，其三为参与者。

(2)设定关键问题。对问题的设定取得一致性。

(3)列举因素之间的相关性。在解释结构模型的有向连接图中，以节点 S i表示系统中的各要素，以带箭头的有向线段表示要素间的相互关系。如下图所示，此系统主要由3要素构成，分别为 S1、S2 与 S3，依据箭头的基本指向，从中可以得出，其中的 S1会影响到S2，而其中的S2则会影响到S3，而对于S3来讲，其与 S1之间呈现彼此互影响的关系。

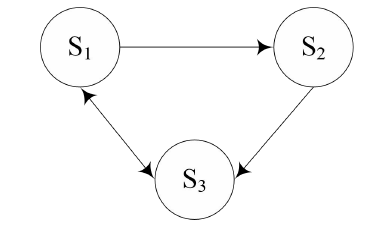
▲有向连接图

（4）建立邻接矩阵。邻接矩阵是表示要素间关系的方阵。若Si对Sj有影响，则 aij为 1，若Si对Sj无影响，则aij为0。即：

结合公式所给出的具体规则，相比于上面的有向连接图，与之呈现对应状态的3阶方阵表达式即：

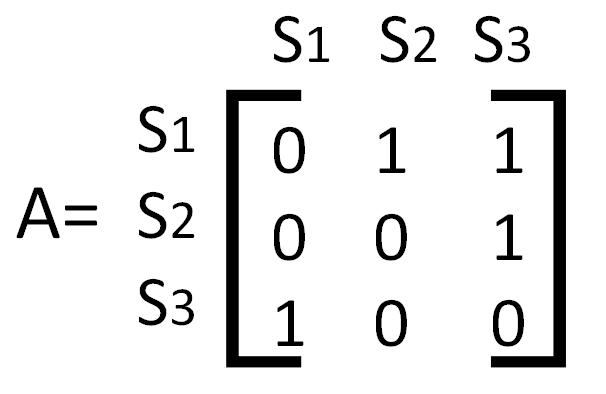
（5）计算可达矩阵及骨架矩阵。可达矩阵描述的是要不同因素之间，他们经过不同路径任意次的传递性二元关系方阵。邻接矩阵 A，以及可达矩阵 M，均是 n 阶 0-1 方阵。他们同时也符合布尔矩阵的运算法则（布尔代数规则：0+0=0,0+1=1,1+0=1,1+1=1,0×0=0,0×1=0,1×0=0,1×1=1）通过算邻接矩阵A，它能够得到可达矩阵为M，计算公式如下：

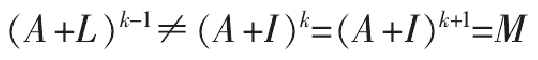
（6）建立骨架矩阵。通过对可达性矩阵的分解（有区域分解和级间分解），即可建立骨架矩阵。

（7）建立ISM模型。根据各要素的实际意义，将骨架矩阵直接转化为解释结构模型。

近年来，随着建筑队伍的不断发展壮大，工程建设过程中的安全事故和人员伤亡数量一直不容乐观。因此，找出影响建筑工人安全意识的关键因素，分析各因素的内在关系以及各因素对建筑工人安全意识发展的影响过程，能为提高建筑工人的安全意识，减少建筑安全事故的发生提供有益的参考。下面就以分析某项目建筑工人安全意识影响因素为例进行ISM的介绍。

（1）建立ISM小组，讨论后最终确定了建筑工人安全意识13个影响因素，如下图所示。

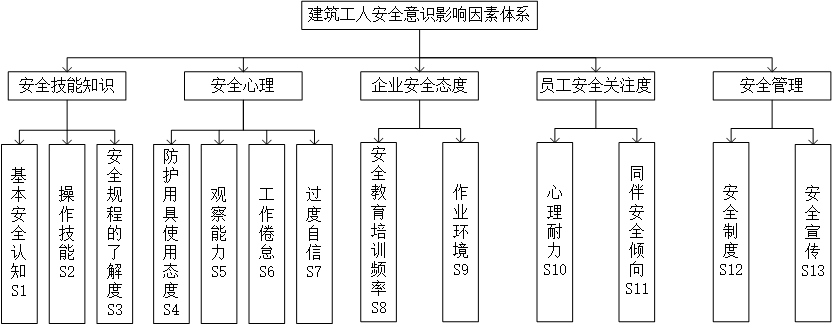
▲建筑工人安全意识影响因素体系

（2）ISM小组讨论得到影响建筑工人安全意识的13个要素间的结构关系，从而得到对应的邻接矩阵A。

（3）根据邻接矩阵计算得到可达矩阵M。

（4）通过对可达矩阵M分解，建立ISM模型，如下图所示。

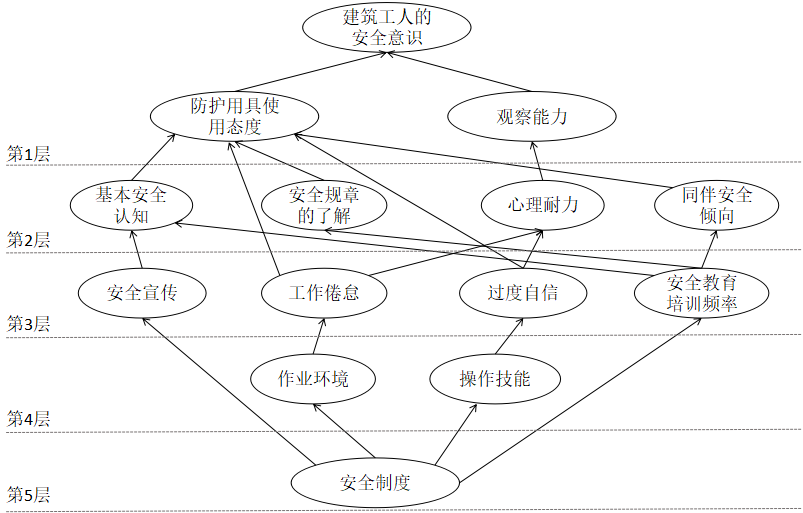
▲建筑工人安全意识影响因素的ISM模型

根据建筑工人安全意识影响因素的ISM模型可看出，影响建筑工人安全意识直接因素是防护用具使用态度和观察能力，其它为间接影响因素，安全制度为影响建筑工人安全意识的根本因素。

ISM模型适用于变量众多、关系复杂而结构不清晰的系统分析中。实现了系统结构的模型化，得到影响问题的直接因素、间接因素和根本因素，明确问题的层次和整体结构，从而提高对问题的认识和理解程度。